|
|
At the bottom of the previous page we saw a picture of the first ten product curves. Product curves are important because every possible way of multiplying one number by another is represented on one of them.
But it turns out that they are only a special case of a more general phenomenon. Their properties are due to the fact that they are located at certain fixed distances from certain angles. As we will see, other curves which are located at fixed distances from other angles have similar properties.
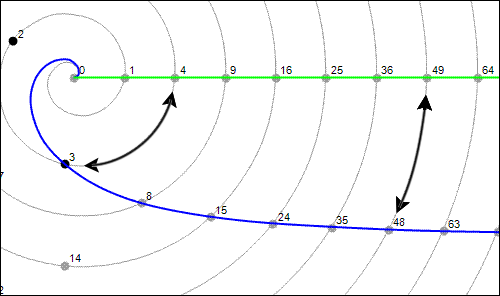
To illustrate these ideas, let's look at product curve S – 1, shown here in blue. It is located at a fixed distance from angle zero, shown in green..
|
|
|
 |
|
| Vortex |
 |
| To draw the green line with Vortex, enter "ang 0" in the command window. To draw the blue curve, enter "s – 1". |
|
|
|
| Figure 1 |
|
|
At first glance the green and blue lines appear to converge at the left. But if we measure the distance between them using the spiral itself as our tape measure, the lines are always one unit apart. The black arrows show how to do this. The left arrow stretches between 3 and 4, a distance of one. The right arrow stretches between 48 and 49, also a distance of one. Even when the blue curve is at zero, it's separated (for measuring purposes) from the green curve by the piece of the spiral that runs from zero to one. No matter where we measure, the distance is always one.
I call a constant distance of this sort an offset. When a curve is offset from an angle line, I call it an offset curve.
If we zoom out far enough, offset curves look straight. Some of them have so little curvature that we barely have to zoom. For instance:
|
|
|
Background
| To read more about angles, go here. |
 |
|
|
|
 |
 |
|
Details
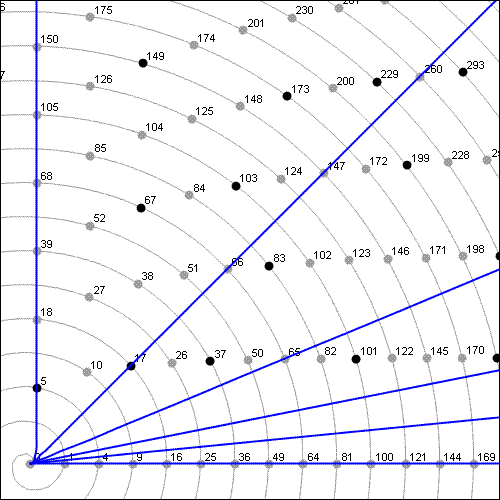
| Curve S is the only truly straight offset curve. All the others are curved, however slightly. For instance, the offset curve for angle 1/16 shown at left changes direction by 1/16 rotation as it travels from zero to infinity. |
 |
|
|
| Vortex |
 |
To draw these curves with Vortex, enter:
coe 1 0 0
coe 4 1 0
coe 16 1 0
coe 64 1 0
coe 256 1 0
coe 1024 1 0 |
|
|
|
| Figure 2 |
|
|
The blue lines in Figure 2 are the first offset curves of angles 0, 1/64, 1/32, 1/16, 1/8, and 1/4.
Offset curves are important because some of them are composite. When I say that a curve is composite I mean that all the integers on them (except for the first, which is always zero, and the second, which may be prime) are non-prime. Moreover, we can predict the factorization of any integer on such curves just from knowing its location.
Every rational angle has composite offset curves.
When I say "rational angle," I mean an angle whose measurement in rotations is a rational number: 1/2 rotation, 1/3 rotation, 1473/2076 rotation, etc.
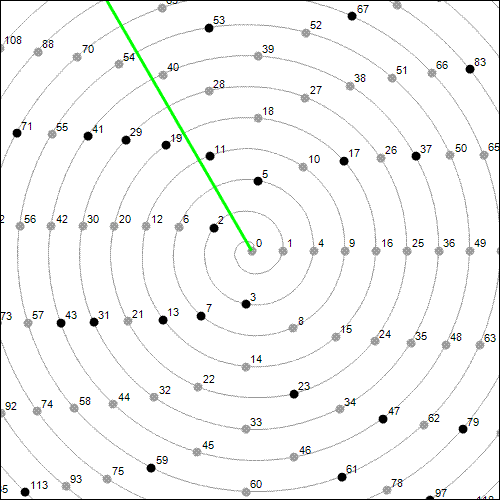
Here, for example, marked in green, is the 1/3 angle (120 degrees): |
|
|
 |
|
| Vortex |
 |
| To draw this angle with Vortex, enter "ang 1/3" in the command window. |
|
|
|
| Figure 3 |
|
|
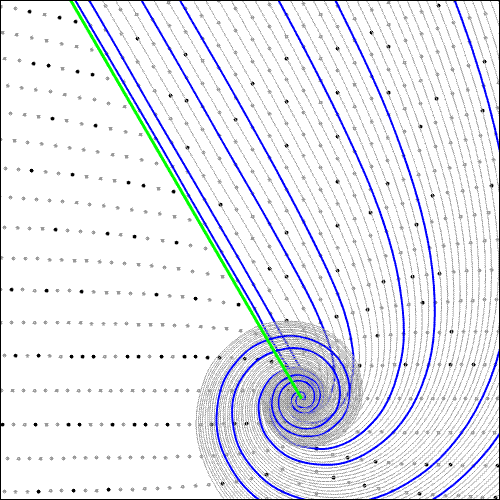
And here are a few of its offset curves:
|
|
|
|
 |
|
| Vortex |
 |
| To draw these curves with Vortex, enter "off 1/3" in the command window. |
|
|
|
| Figure 4 |
|
|
The blue offset curves are composite. (To avoid misunderstanding, let me say again that the first integer on a composite curve is zero, the second may or may not be prime, and the rest are composite.)
As I said a moment ago, every rational angle has blue offset curves of this type. Here, for example, is angle 29/33: |
|
|
|
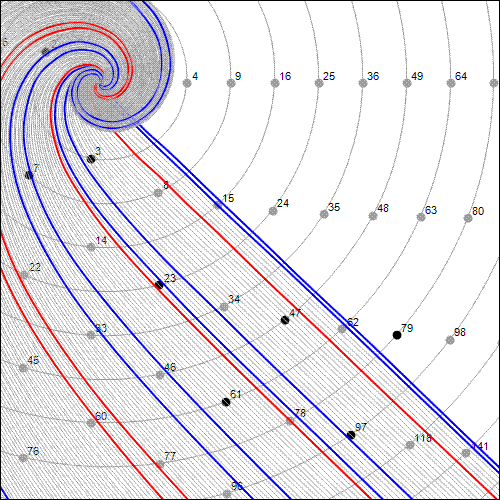 |
|
| Vortex |
 |
| To draw these curves with Vortex, enter "off 29/33" in the command window. |
|
|
|
| Figure 5 |
|
|
In Figure 5 you see something new: red curves. Like blue curves, red ones are composite. But red and blue sequences are composite for different reasons, so I distinguish them by color.
|
|
|
|
| One last example. Here are the first few offset curves for angle 1/4. |
|
|
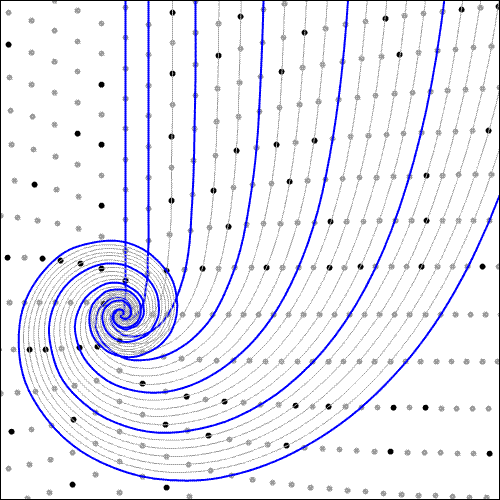 |
|
| Vortex |
 |
| To draw these curves with Vortex, enter "off 1/4" in the command window. |
|
|
|
| Figure 6 |
|
|
| I have a special reason for including angle 1/4 on this page. When I first wrote this website in 2003, I didn't realize that every rational angle has composite curves. Therefore I was puzzled by the prominent columns of non-prime numbers that march north and south from the center of the spiral, and I published the following picture as a mystery to be solved later: |
|
|
|
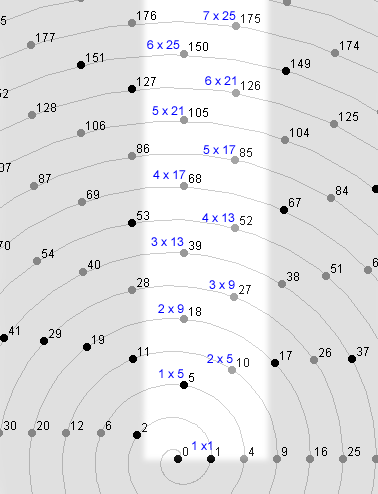 |
Figure 7 |
|
|
|
|
| Today, as I write this page in 2007, I'm happy to say that the mystery is solved. The highlighted numbers in figure 6, with their predictable factorizations, belong to the first two "blue" offset curves of angle 1/4 which were shown in Figure 6. |
|
|
|
 |
|
|
|
Details
Offset curves exhibit many interesting patterns based on the relationships between their angles, their offsets, the factorizations of integers found on them, and the functions that generate them.
Offset curves (as opposed to the integer sequences found on them) are real-valued quadratic functions in which the coefficient of x2 is a perfect square. When they are drawn on Cartesian coordinates they are the non-negative portions of the right limbs of parabolas. I use the following functions to graph them:
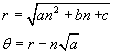
As time permits I plan to add pages to this website which describe the properties of these curves.
In the meantime a great deal can be learned about them by examining them with Vortex, which may be downloaded here. |
|
|
|
|
 |
|
|
|
|
 |
| Copyright © 2003, 2007 Robert Sacks |
|
|